摘要:在本节中,你将学习如何在 Python 中找出两个或多个集合之间的对称差集。
集合对称差集简介
两个 集合 之间的对称差集是由那些仅属于其中一个集合,而不属于它们交集的元素所组成的集合。
假设你有以下集合 s1 和集合 s2:
s1 = {'Python', 'Java', 'C++'}
s2 = {'C#', 'Java', 'C++'}集合 s1 和集合 s2 的对称差集得到的是下面这个集合:
{'C#', 'Python'}从输出结果中你可以清楚地看到,返回集合中的元素要么在集合 s1 中,要么在集合 s2 中,但不在它们的交集中。
下面的维恩图展示了集合 s1 和集合 s2 的对称差集:
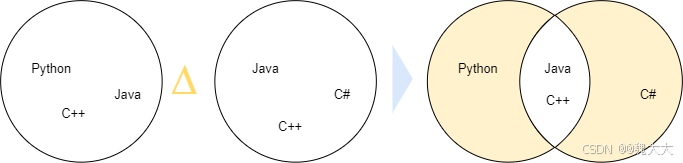
在 Python 中,你可以通过使用集合的 symmetric_difference() 方法或对称差集运算符(^)来找出两个或多个集合的对称差集。
### 使用 symmetric_difference() 方法来找出集合的对称差集
集合(Set)类型有 symmetric_difference() 方法,该方法会返回两个或多个集合的对称差集:
new_set = set1.symmetric_difference(set2, set3,...)例如,以下操作找出了集合 s1 和集合 s2 的对称差集:
s1 = {'Python', 'Java', 'C++'}
s2 = {'C#', 'Java', 'C++'}
s = s1.symmetric_difference(s2)
print(s)输出:
{'C#', 'Python'}请注意symmetric_difference() 方法会返回一个新的集合,并且不会修改原始的集合。
使用对称差集运算符(^)来找出集合的对称差集
除了使用集合的 symmetric_difference() 方法之外,你还可以使用对称差集运算符(^)来找出两个或多个集合之间的对称差集:
new_set = set1 ^ set2 ^...下面的示例展示了如何对集合 s1 和集合 s2 使用对称差集运算符(^):
s1 = {'Python', 'Java', 'C++'}
s2 = {'C#', 'Java', 'C++'}
s = s1 ^ s2
print(s)输出:
{'Python', 'C#'}symmetric_difference() 方法与对称差集运算符(^)的对比
symmetric_difference() 方法可以接受一个或多个可迭代对象,这些可迭代对象可以是字符串、列表或字典。
如果这些可迭代对象不是集合,该方法会先将它们转换为集合,然后再返回它们的对称差集。
以下示例展示了如何使用 symmetric_difference() 方法来找出一个集合和一个列表之间的对称差集:
scores = {7, 8, 9}
ratings = [8, 9, 10]
new_set = scores.symmetric_difference(ratings)
print(new_set)输出:
{10, 7}然而,对称差集运算符(^)仅适用于集合。如果你将它用于非集合的可迭代对象,就会出现错误。例如:
scores = {7, 8, 9}
ratings = [8, 9, 10]
new_set = scores ^ ratings
print(new_set)错误:
TypeError: unsupported operand type(s) for ^: 'set' and 'list'总结
两个或多个集合的对称差集是由那些仅属于其中某些集合(即不在所有集合的交集中)的元素所组成的集合。
使用集合的
symmetric_difference()方法或对称差集运算符(^)来找出两个或多个集合的对称差集。
